|
|
Noun Phrases
Frege’s predicate logic was a crude attempt to marry the analysis of predicates to propositional logic. Predicate logic splits propositions into predicates and their arguments. Whether a proposition is represented as a single variable p, or a predicate F(x), the logical expressions bare little structural resemblance to sentences in natural languages. Generalized quantifier theory takes us a step closer to a logic that mirrors expressions in natural languages.
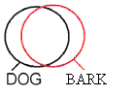
Predicate logic supplies a semantic analysis for the quantifiers ∀ and ∃:
∀x(DOG(x)—>BARK(x))
‘For all x, if x is a dog then x barks’
All dogs bark.
∃x (DOG(x) & BARK(x))
‘There is at least one thing x such that x is a dog and x barked’
A dog barked.
Quantified predicates have the general form:
Quantifier |
NP predicate |
Connective |
VP predicate |
Kearns invites us to extend this analysis to the quantifier most. Following the traditional analysis of quantifiers produces the following analysis of the sentence Most dogs bark.
Quantifier Most x |
NP predicate DOG(x) |
Connective __??__ |
VP predicate BARK(x) |
The question is which connective should we use to fill in this blank. We try each of the traditional logical connectives in turn (&, v, —> and <—>):
Most x(DOG(x) & BARK(x))
DOG(x) |
BARK(x) |
DOG(x) & BARK(x) |
T |
T |
T |
T |
F |
F |
F |
T |
F |
F |
F |
F |
Using the conjunction connective predicts the sentence Most dogs bark is only true where most of the things in the universe of discourse are both dogs and barking. If we don’t restrict the universe by context, then this analysis is only true where most things are barking dogs. This is clearly the wrong analysis for this sentence.
Suppose we appeal to pragmatics to constrain the universe of discourse. Now we are in a situation where dogs have become the topic of the discourse, and we assert that most things in the doggy universe bark. This is the interpretation we are looking for, but we lack an explicit method of restricting the discourse universe to the doggy verse. This is what Generalized Quantifier Theory does.
Generalized Quantifier Theory
Generalized Quantifier Theory provides a uniform treatment for quantified expressions by analyzing them in terms of set relations. The philosopher Richard Montague first developed a general account of quantifiers in English (Montague 1973). His analysis served as the foundation for what has come to be known as Montague Semantics, the best known approach to providing a formal semantics for natural language. Montague’s basic idea for the treatment of quantifiers was to specify the relation between a restrictor set identified by the NP to the predicate set identified by the VP. We can draw on set theory for a guide to the possible set relations.
|
D = B |
The sets D and B have the same members. |
|
D ⊂ B |
The members of set D are a proper subset of set B. |
|
D ⊆ B |
The members of set D are a subset of the members of set B. |
|
|D| |
The cardinality or number of members in set D. |
|
|D| > |B| |
The number of members of set D is greater than the number of set B members. |
|
|D| ≥ |B| |
The cardinality of set D is greater or equal to the cardinality of set B. |
|
D ∩ B |
The individuals that are members of both sets D and B. |
|
D – B |
The members of set D that are not members of set B. |
Generalized Quantifier theory treats the set identified by the NP as a restricted quantifier. The NP restricts the discourse universe to the relevant set, say the set of dogs. The quantifier then picks out a number of individuals from this restricted set, e.g., all the dogs, most dogs, two dogs. This approach treats the quantifier as part of the NP rather than separate from the rest of the proposition. This treatment results in a syntax for quantifiers as follows:
[Most x: DOG(x)] BARK(x)
[All x: DOG(x)] BARK(x)
[No x: DOG(x)] BARK(x)
We can use the set relations to supply the semantics for the restricted quantifiers.
Strong NPs |
All Ds B |
D ⊆ B |
All dogs bark. |
Proportional |
Most Ds B |
|D ∩ B| > |D – B| |
Most dogs bark. |
|
Few Ds B |
|D – B| > |D ∩ B| |
Few dogs bark. |
Weak NPs |
No Ds B |
|D ∩ B| = 0 |
No dogs bark. |
Intersective |
A D Bs |
|D ∩ B| ≥1 |
A dog barks. |
|
Some Ds B |
|D ∩ B| ≥2 |
Some dogs bark. |
|
Four Ds B |
|D ∩ B| = 4 |
Four dogs bark. |
|
Many Ds B |
|D ∩ B| = many |
Many dogs bark. |
|
Several Ds B |
|D ∩ B| = several |
Several dogs bark. |
|
Few Ds B |
|D ∩ B| = few |
Few dogs bark. |
|
A few Ds B |
|D ∩ B| = a few |
A few dogs bark. |
We can apply this semantics to the sentence Most dogs bark. The logical syntax translates this sentence as:
|
[Most x: |
DOG(x)] |
BARK(x) |
|
Quantifier |
Restriction |
Predicate |
The semantics specifies the truth conditions for the syntax. Consulting the table above, the semantics will evaluate the syntactic expression as true if the set relation |D ∩ B| > |D – B| is true, i.e. the number of individuals that are barking dogs is greater than the number of non-barking dogs.
|

|
Now we have a formal means of restricting the universe of discourse to the relevant sets. Montague’s analysis provides a uniform treatment for the quantifiers that mirrors the syntactic structure of English. Other examples with restricted quantifier translations include:
Layla ate a few pretzels.
[Few x: PRETZEL(x)] ATE(l,x)
John found a lost dog.
[A x: DOG(x) & LOST(x)] FOUND(j,x)
Most dogs that Mary finds are friendly.
[Most x: DOG(x) & FIND(m,x)] FRIENDLY(x)
Scopal Ambiguity
The restricted quantifier notation that Kearns introduces makes it easy to predict when scopal ambiguity will occur between quantified NPs. In fact, the logic predicts that any sentence with two or more quantified expressions (or negation) will result in a sentence with scopal ambiguity. Consider the scopal ambiguity in following sentences:
Every woman loves a man.
[Every x: WOMAN(x)] [A y: MAN(y)] LOVES (x,y)
[A y: MAN(y)] [Every x: WOMAN(x)] LOVES (x,y)
Many women love a few men.
[Many x: WOMAN(x)] [A few y: MAN(y)] LOVE (x,y)
[A few y: MAN(y)] [Many x: WOMAN(x)] LOVE (x,y)
Most women love two men.
[Most x: WOMAN(x)] [Two y: MAN(y)] LOVE (x,y)
[Two y: MAN(y)] [Most x: WOMAN(x)] LOVE (x,y)
Quantified NPs do not always produce a scopal ambiguity with negation.
Not many dogs barked.
[~ Many x: DOG(x)] BARK(x)
Many dogs did not bark.
[Many x: DOG(x)] ~ BARK(x)
We can negate the quantified NP, as in the first example. In these contexts, negation produces a complementary set. If Many dogs barked has the interpretation |D ∩ B| = many, then Not many dogs barked has the interpretation |D ∩ B| = ~ many. If few is the complement of many, than ~ many is semantically equivalent to few. Therefore, the sentence Not many dogs barked also has the interpretation |D ∩ B| = few.
The second sentence has the interpretation |D ∩ ~B| = many. This interpretation results in the intersection of the DOG set with the complement to the BARK set. The result is equivalent to the interpretation of the first sentence (|D ∩ B| = ~ many) because the intersection of the nonbarking set with the DOG set picks out many of the dogs, and the intersection of the barking set with the DOG set does not pick out many dogs. We conclude:
|D ∩ B| = ~ many ≡ |D ∩ ~B| = many
The quantifier many does not produce a scopal ambiguity with negation. Do other quantifiers produce scopal ambiguity with negation?
We can negate the NP directly, which produces a null intersection between the restrictor set DOG and the predicate set BARK.
No dogs barked.
[No x: DOG(x)] BARK(x)
English uses the negation markers no and not in different contexts. The negation marker no is used in response to questions or commands, as well as serving as a negative quantifier on NPs. The negation marker not is used to negate propositions as well as to negate quantifiers as in the example with not many. No is referred to as anaphoric negation, while not is referred to as propositional negation. A puzzle arises as to why English uses not with quantified NPs. Spanish does not.
Specific and nonspecific NPs
Indefinite NPs create an ambiguous reading between specific and nonspecific referents with propositional attitude verbs such as know, believe, think and hope. These verbs express an attitude that the subject adopts toward the proposition in the verb’s complement. The complement phrases describe the mental contents of someone rather than an objective state of affairs. In these contexts indefinite NPs have both specific and nonspecific interpretations.
|
specific |
Mary wants to marry a Norwegian (his name is Olaf). |
|
nonspecific |
Mary wants to marry a Norwegian (anyone from Oslo will do). |
These different interpretations correspond to differences in the scope of the propositional attitude verb and the quantified NP:
‘Mary wants to marry a Norwegian.’
|
specific |
[A x: NORWEGIAN(x)] WANT(m, MARRY(m, x)) |
|
nonspecific |
WANT(m,[A x: NORWEGIAN(x)] MARRY(m, x)) |
We find a similar ambiguity in modal contexts:
‘Mary might have married a Norwegian.’
|
specific |
[A x: NORWEGIAN(x)] ◊ MARRY(m, x) |
|
nonspecific |
◊ [A x: NORWEGIAN(x)] MARRY(m, x) |
Negation also creates a scopal ambiguity with indefinite NPs:
‘Mary didn’t marry a Norwegian.’
|
specific |
[A x: NORWEGIAN(x)] ~ MARRY(m, x) |
|
nonspecific |
~ [A x: NORWEGIAN(x)] MARRY(m, x) |
In all of these cases, the specific reading carries an existential commitment. Mary has identified a Norwegian who actually exists. The nonspecific readings do not make this commitment. Mary may never find a Norwegian to marry.
Indefinite NPs do not exhibit a difference in existential commitment in combination with other quantifiers. They do, however, still exhibit an ambiguity between specific and nonspecific readings:
‘Everyone saw a Norwegian.’
|
specific |
[A x: NORWEGIAN(x)] ∀y SAW(y,x) |
|
nonspecific |
∀y [A x: NORWEGIAN(x)] SAW(y,x) |
The contrast between specific and nonspecific in each of these examples is connected to a reference or lack of reference to a single individual. These examples also highlight the contrast between specificity and definiteness. The first sentence in each example has an indefinite NP that refers to a specific entity.
Strong versus Weak NPs
Our table marks a distinction between Strong and Weak quantifiers that results in the distinction between strong and weak NPs. Strong NPs are defined in terms of a proportional relation between sets, whereas the Weak NPs are defined by the intersection between sets. Proportional relations are asymmetric relations. If seventy percent of dogs bark, then we cannot conclude that seventy percent of barking animals are dogs. What other animals bark?
Intersective relations are symmetric relations. The intersection of set D with set B is identical to the intersection of set B with set D. More formally |D ∩ B| = |B ∩ D|. If several dogs bark, then we can conclude that several barking animals are dogs.
It is all well and good to note these mathematical differences. It would be surprising if this mathematical difference actually predicted linguistic differences. We have no obvious reason to predict a correspondence between math and language.
Milsark (1974, 1977) observed that strong and weak NPs in English had different contexts of use. Existential sentences beginning with There is/are require weak NPs. Existential sentences are unacceptable with strong NPs. This restriction is referred to as a definiteness effect.
There is a fly in my soup.
There were several flies in the soup.
There were many flies in the soup.
There were four flies in the soup.
* There was every fly in the soup.
* There were most flies in the soup.
Definite NPs denote definite or specific entities. Names, possessive NPs such as John’s jacket, demonstrative NPs such as that boulder, those tablets, and referring pronouns are all examples of definite NPs. They are not acceptable in existential sentences.
* There was Terry in the garden.
* There was that dog in the garden.
* There were they/them in the garden.
The existential test is complicated by different types of there be sentences. Kearns discusses the following types:
Basic existential there be.
Deictic there be, used to pick out the location of the NP (Lakoff 1987).
There’s Harry with his red hat on.
Task there be, in the frame there be NP to VP.
There are the dishes left to wash.
List there be.
Who’s available Saturday?
There’s Ian, Mary and Henry.
Lakoff (1978:468) points out several syntactic differences between existential and deictic there be sentences.
Existential there can be used in tag questions; deictic there cannot:
|
Existential: |
There was a dog in the garden, wasn’t there? |
|
Deictic: |
* There’s Harry with his red hat on, isn’t there? |
Existential there can be used in raising constructions; deictic there cannot:
|
Existential: |
There was believed to have been a dog in the garden. |
|
Deictic: |
* There is likely to be Harry with his red hat on. |
Existential there can be negated; deictic there cannot:
|
Existential: |
There weren’t any dogs in the garden. |
|
Deictic: |
* There isn’t Harry with his red hat on. |
Deictic there alternates with here; existential there does not:
|
Existential: |
* Here is a dog in the garden. |
|
Deictic: |
Here’s Harry with his red hat on. |
Deictic there can be stressed; existential there cannot:
|
Existential: |
* THERE’S a dog in the garden. |
|
Deictic: |
THERE’S Harry with his red hat on. |
There be constructions have a long history of linguistic investigation (Lakoff 1987). The main explanation for the strong NP constraint in these sentences is based on the idea that there be sentences assert the existence of a referent named by the NP. This assertion clashes with the use of strong NPs which presuppose the existence of the entity they denote.
Consider the sentence: There were most dogs in the garden.
Existential be asserts the existence of the following NP’s referent most dogs. The trouble is that the strong quantifier most presupposes the existence of the doggy set it restricts. This presupposition clashes with the existential assertion of be.
Few and Many
The quantifiers few and many have both strong and weak readings. The strong reading for few has a partitive sense, which can be rephrased as a few of the fleas. This reading suggests a quantity that bears a specific relation to the size of the whole group:
No flies and few fleas survived the treatment.
The weak reading for few merely suggests that an absolute small number is involved as opposed to a relatively small number:
The house seemed clean and Lee found few fleas.
Compare these sentences in the existential context:
There were few fleas in the house.
* There were no flies and few fleas that survived the treatment.
This difference is less clear for many. Many speakers don’t acknowledge a strong or proportional reading for many. The strong reading has an interpretation that is similar to most. Many denotes a proportion that is greater than half, while most denotes a proportion much greater than half.
Many students preferred the assignments in the book.
These judgements are sensitive to the absolute size of the group. Compare your reaction if the class has 300 students as opposed to 12 students. It seems correct to apply many when the whole contains fewer than ten members. Many appears to have a proportional reading when the background set is medium sized. Which interpretation does many have in an existential sentence?
There are many students in my class.
Plural NPs and Groups
We have been using a distributive analysis for quantified expressions–the predicate is distributed to each individual:
6. Three cups broke.
[Three x: CUP(x)] BREAK(x)
The red cup broke.
The yellow cup broke.
The blue cup broke.
The distributive treatment parcels the action over each cup in succession. We can also analyze the predicates in (5) distributively:
7a. [A x: NORWEGIAN(x)] ∀y SAW(y,x)
Harry saw Olaf.
Ann saw Olaf.
Rebecca saw Olaf, etc.
b. ∀y [A x: NORWEGIAN(x)] SAW(y,x)
Harry saw Olaf.
Ann saw Sven.
Rebecca saw Olaf and Sven, etc.
Collective Predication
Collective predication refers to predication involving a group of individuals:
8a. The boys greeted one another on the street.
b. Sally and Harry met at the beach.
c. The forest surrounds the castle.
A group collective refers to a group with identifiable members. The members of the group carry out the action collectively. The predications do not apply to a single individual:
9a. The boys greeted one another on the street.
b. The leaders debated the compensation proposal.
Substance collectives refer to a substance. Although substances like sand or flour have individual particles, we do not recognize their individual identities. Even a crowd of people can form a substance as long as we do not care about the specific individuals who make up the crowd. Predicates like surround and disperse can be applied to substances:
10a. The water surrounded the forest.
b. The crowd dispersed slowly.
Collective predication applies to both group collective predicates and substance collective predicates. The individuals in the group interact with one another in group collective predications, but not in substance collective predications.
The distributive analysis cannot be used for collective predicates with quantified plural NPs:
14. A thousand trees surrounded the castle.
[A thousand(x): TREE(x)] [The y: CASTLE(y)] SURROUND(x,y)
We can use set theory to introduce a variable that stands for the whole group. This produces a collective interpretation:
15. [A X:|X| = 1,000 & ∀y (y ∈ X —> TREE(y)] [The z: CASTLE(z)] SURROUND (X, z)
Plural NPs may have both distributive and collective readings, depending on the context:
16a. The apples in this barrel weigh at least six ounces.
b. The apples in this barrel weigh at least sixty pounds.
The English quantifiers every and all also differ in their ability to combine with collective predicates. Every can only be used with distributive predicates. All can have both distributive and collective interpretations:
17a. *Every piece here fits together to make a picture.
b. All these pieces fit together to make a picture.
c. The price of all these pieces is $20.00.
d. The price of every piece here is $20.00.
Kearns provides multiple interpretations for the sentence Two men lifted a rock:
18a. [Two x: MAN(x)] [A y: ROCK(y)] LIFT(x,y)
b. [A y: ROCK(y)] [Two x: MAN(x)] LIFT(x,y)
c. [A X: |X| = 2 & ∀x (x ∈ X —> MAN(x)] [A y: ROCK(y)] LIFT(X,y)
Discussion (de Swart 225)
Consider the following sentences:
i) Mary believes that a professor was caught shoplifting.
ii) Chris wants to marry a Spanish linguist.
Although both of these sentences contain indefinite NPs rather than definite NPs, they have an ambiguity due to a propositional attitude verb. Translate each sentence into logical expressions that spell out the ambiguity involved. Explain informally how the interpretation of the indefinite NP in these opaque contexts leads to different interpretations of the sentences.
References
Montague, Richard. 1973. The proper treatment of quantification in ordinary English. In J. Hintikka, J. M. E. Moravcsik & P. Suppes (eds.), Approaches to Natural Language, pp. 221-242. New York: Springer.
Rueland, Eric & Alice ter Meulen, eds. 1987. The Representation of (in)definiteness. Cambridge, MA: MIT Press.