|
 U |
Predicate Logic
Propositional logic can make truth assignments for an infinite number of sentences as well as show which sentence are logically equivalent, but it fails to derive the meaning of a sentence from the meaning of its constituents. Propositional logic does not have the means of capturing the meaning of sentential operators like probably, unfortunately or apparently. Nor can it deal with connectives like although, because or after.
Predicate logic provides a start in this direction. Predicate logic derives the meaning of a sentence from the meaning of its predicate and arguments. The predicates in predicate logic do not correspond to the predicates in a natural language. Kearns provides some examples of these differences.
24 |
Sentence |
Predicate |
Arguments |
|
a |
Brigitte is taller than Danny. |
... is taller than ... |
Brigitte |
Danny |
b |
Alex is Bill’s henchman. |
... is ...’s henchman |
Alex |
Bill |
c |
Fiji is near New Zealand. |
... is near ... |
Fiji |
New Zealand |
The German philosopher Gottlob Frege invented a system for representing predicates as expressions with ‘open places’ that could be filled in by arguments (Frege 1879). This system is known as first-order predicate logic because the predicates range over individuals and not over higher-order entities like properties and relations. Predicates can have any number of arguments. The convention in predicate logic is to represent the predicate in capital letters and each arguments with a lower case letter.
26 TALLER (b, d)
HENCHMAN (a, b)
NEAR (f, n)
Most predicates are semantically incomplete without arguments. Weather predicates such as RAIN and SNOW are exceptions. One-place predicates include WALK and RUN; two-place predicates are LOVE and KILL; and three-place predicates are GIVE and PUT. Predicates in predicate logic take a fixed number of arguments. Some predicates in natural language alternate between one or more arguments, e.g., break and melt. Predicate logic insists on the correct number of arguments to produce a well-formed formula.
Logical predicates can be derived from a wide variety of lexical categories:
31 |
adjective |
TALL, PURPLE, GREEK |
|
preposition |
NEAR, ON, BEHIND |
|
noun |
MOTHER, DOG, CORACLE |
|
verb |
COUGH, SEE, READ |
We can apply all the apparatus of propositional logic to predicate logic. Predicates combine with arguments to produce propositions. We can then use the connectives from propositional logic (e.g., negation, conjunction, etc.) to produce more complex propositions. The following sentences in English and their translations into predicate logic demonstrate the use of connectives with predicates:
3. de Swart (1998:75)
Milly doesn’t swim, but Jane does (swim).
~ SWIM(m) & SWIM(j)
If Copenhagen is nice, Milly is happy.
NICE(c) —> HAPPY(m)
The Semantics of Predicate-Argument Structures
Predicate logic, like propositional logic, reduces the meaning of a proposition to its truth value. To maintain a compositional theory of meaning, we need a method of combining predicates and arguments to produce a proposition with a truth value. We must find an interpretation of the arguments and predicates, and the way they combine in predicate-argument structures.
Individual constants are arguments that point to a single individual in the universe of discourse. The names Brigitte and Alex that we saw above are examples of individual constants. Each proper name points to a single entity. The logical model if far simpler than the names we use in ordinary speech. We know many individuals share common names such as Emily and Josh. The idea in predicate logic is to insist that each individual in the universe is unique. This fiction allows us to treat names as rigid designators that refer uniquely.
Individuals are semantic primitives in predicate logic. We don’t have to worry about what they are exactly. We simply assume they exist and that we can name/identify each of them. The set of individuals defines the universe of discourse U for the model M. All of the concepts in predicate logic, including the meaning of the predicates, are defined in relation to this universe.
These assumptions raise some interesting issues. One is the problem of maintaining reference to a single individual whose material composition changes constantly. Most of the cells in our bodies have been replaced several times since birth and yet we assume this process is irrelevant for individuation. We are still the same person regardless of any biological or psychological changes we have undergone, even though we may be five or six times bigger than at birth.
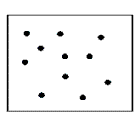
The model also assumes we have some way to specify what the constants in the language refer to. We can assume there is an interpretation function I, which picks out the appropriate denotation in the universe of discourse. Let α stand for an individual constant. The interpretation function maps α onto one of the individuals in the universe of discourse: I(α) ∈ U. One way to visualize this universe is shown below.
|
 U |
Given this universe, we can define properties by picking out the individuals that have those properties. We may not be able to define what barking is, but we can characterize barking by pointing to barking individuals. This procedure provides an extensional definition for properties by listing the individuals who exhibit the specific property. One-place properties are modeled as sets of individuals: the property of barking is defined by the set of individuals that bark. More formally, for a one-place predicate α, the interpretation function I maps α onto a subset of the universe of discourse U: I(α) ⊆U. We can formally define barking in our model as
[ BARK]M = {x ∈ U | BARK(x)}
We can visualize this interpretation as shown below.
|
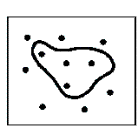 U |
Bark |
The main limitation with an extensional approach of this sort is that it gives the same interpretation to all predicates that have the same extension. For example, if all the round objects happen to be apples and all the apples happen to be round, then the two predicates apple and round point to the same set of individuals in the universe of discourse. Extensional interpretations only approximate meaning in a natural language. The extensional approach has to be enriched by appealing to intensional definitions if we want to provide a better account for meaning in natural language.
2.4.1 The Universal Quantifier
Arguments in predicate logic can take various forms. Individual variables refer to different individuals much like pronouns. A sentence like He walks would be represented in predicate logic as
WALK(x)
By itself, this expression doesn’t form a complete proposition. The free variable doesn’t point to anything. An expression with free variables forms an open proposition. To evaluate its truth value we have to specify the individual or individuals the variable picks out. One way to form a complete proposition from an open proposition is to bind the variable’s reference to some set of individuals. A quantifier is used to bind free variables in open propositions. For example, the sentence Everyone walks has a truth value. We can check if all the individuals we know (Brigitte, Alex, ...) walk. The sentence Everyone walks can be represented in predicate logic as
∀x (WALK (x))
The addition of the quantifier binds the free variable and produces a closed proposition. The symbol ‘∀’ is used for the universal quantifier. The quantifier appears with a copy of the variable which is its target. The part of the expression the quantifier binds is marked by parentheses to indicate the scope of the quantifier.
The translation of quantified expressions into predicate logic can be tricky. Kearns discusses the sentence Every dog barks. It is tempting to write this sentence as
∀d (BARK (d))
Using the ‘d’ to stand for DOG obscures the proposition that the things being quantified are dogs. This can be expressed by a separate proposition:
DOG(x)
We need to combine the idea that x is a dog with the idea that x barks. Material implication allows us to express this idea.
DOG(x)—>BARK(x)
If x is a dog then x barks. Binding the free variable with the universal quantifier produces the expression
∀x(DOG(x)—>BARK(x))
‘For all x, if x is a dog then x barks’
This proposition is true even if there are no dogs. The truth table for material implication predicts this outcome.
52 |
DOG (x) |
BARK (x) |
DOG (x) —> BARK (x) |
|
|
T |
T |
|
T |
|
T |
F |
|
F |
|
F |
T |
|
T |
|
F |
F |
|
T |
If there are no dogs then the proposition DOG (x) is false. The material implication is still true in this case. The proposition Every dog is barking is logically equivalent to There is no non-barking dog. One thing to remember from this example is that the universal quantifier is associated with material implication.
McCawley (1981:98) cites Vendler (1967) in pointing out some differences between the quantifiers in English that are commonly used to translate the universal quantifier of predicate logic. The following sentences would usually have the same translation into predicate logic:
a. All doctors will tell you that Stopsneeze helps.
b. Every doctor will tell you that Stopsneeze helps.
c. Any doctor will tell you that Stopsneeze helps.
d. Each doctor will tell you that Stopsneeze helps.
Sentence (d) suggests a sequence of events, i.e., that you will consult each doctor in turn. The other sentences do not have this commitment. You might be able to get all their opinions simultaneously. This sequential commitment for each leads to differences in acceptability in some cases:
Marge admired each of her husbands.
? Marge admired each of her uncles.
The acceptability judgements depend on the idea that women in our society have husbands in succession, not have uncles at the same time. Each matches the times when Marge was married with the proposition that at that time she admired her current husband.
All differs from each, any and every in that it can be used to designate a ‘group’ rather than quantify over individuals. Consider the sentence
All of the boys carried the piano upstairs.
In one interpretation, each of the boys could take a turn carrying the piano upstairs. In the ‘group’ interpretation, all of the boys together carry the piano upstairs. This example demonstrates an important respect in which all differs from the universal quantifier. The ‘group’ interpretation can result in invalid inferences (c.f. Kutz 2000). Compare the logical inference known as universal instantiation with individual and ‘group’ interpretations:
Individual
All men are mortal.
Socrates is a man.
Therefore, Socrates is mortal.
Group
All of the boys carried the piano upstairs.
George is one of the boys.
Therefore, George carried the piano upstairs.
Quine (1960:138-41) suggested treating any as a universal quantifier with wide scope, whereas every and all have narrow scope:
John didn’t talk to anyone.
∀x ~ (John talk to x)
John didn’t talk to everyone.
~ ∀x (John talk to x)
McCawley cites the following examples from Geach (1972:7) that support Quine’s claim:
You may marry anyone you want to.
∀x may ((you want (you marry x)) —> (you marry x))
You may marry everyone you want to.
may ∀x ((you want (you marry x)) —> (you marry x))
However other uses of any don’t support Quine’s analysis. His analysis doesn’t explain why all or every can be used with almost whereas any cannot:
Almost all of the glasses are cracked.
Almost every student found problem3 difficult.
* John didn’t talk to almost anyone.
It is also difficult to imagine a wide scope treatment for the sentence
Hardly any Americans enjoy opera.
Suffice it to say that the universal quantifier as used in predicate logic only succeeds in translating part of the meaning of the English quantifiers.
2.4.2 The Existential Quantifier
The existential quantifier is the other logical quantifier. It expresses the existence of at least one instance of something. It is written as the symbol ‘∃’. The existential quantifier can be used with singular or plural referents. Kearns provides the following examples:
54 |
A dog barked. |
|
∃x (DOG(x) & BARK(x)) |
|
‘There is at least one thing x such that x is a dog and x barked’ |
|
|
|
Some birds were singing. |
|
∃x (BIRD(x) & SING(x)) |
|
|
|
Louise bought some trashy paperbacks. |
|
∃x (TRASHY(x) & PAPERBACK(x) & BUY(l,x) |
Note that Kearns uses the conjunction connective with the existential quantifier rather than material implication. We don’t want to conclude that A dog barked is true if there are no dogs!
|
DOG (x) |
BARK (x) |
DOG (x) & BARK (x) |
|
|
T |
T |
|
T |
|
T |
F |
|
F |
|
F |
T |
|
F |
|
F |
F |
|
F |
McCawley (1981:102) notes that the existential quantifier is used to translate a/an and some in English. English forces speakers to express number as singular or plural while the existential quantifier is satisfied as long as there is at least one individual with the desired property.
2.4.3 Scopal Ambiguity
Negation can be combined with quantifiers as well as with propositions. Kearns demonstrates two ways to do this
55b ~ ∃x (EAT(c, x))
‘There is no x such that Clive ate x.’
Clive ate nothing.
56 ∃x ~ (EAT(c, x))
‘There is at least one x such that Clive didn’t eat x.’
Clive didn’t eat something.
These examples demonstrate how the order of the quantifiers can affect the meaning of the proposition. Negation comes first in (55b); it has wide scope with respect to the existential quantifier. The existential quantifier has narrow scope in this example; it falls in the scope of negation. My translation for (56) (Clive didn’t eat something) is actually ambiguous. It could be translated into predicate logic by either (55b) or (56). The sentence is an example of scopal ambiguity.
Kearns discusses the classic example of a sentence with scopal ambiguity between the universal and existential quantifiers—Everyone loves someone. This sentence has the two interpretations shown below:
63a ∀x∃y (LOVE (x, y))
‘For every person x, there is at least one person y such that x loves y.’
b ∃y∀x (LOVE (x, y))
‘There is at least one person y such that everyone loves y.’
Note: my text has mistyped the logical expression for (63b).
Logical Equivalences
Kearns points out two logical equivalences between universally quantified propositions and existentially quantified propositions.
57a |
∀x (DOG(x) —> BARK(x)) |
|
‘For every x, if x is a dog then x is barking.’ |
b |
~ ∃x (DOG(x) & ~BARK(x)) |
|
‘There is no x such that x is a dog and x is not barking.’ |
58a |
∃x (DOG(x) & BARK(x)) |
|
‘There is an x such that x is a dog and x is barking.’ |
b |
~ ∀x (DOG(x) —>~ BARK(x)) |
|
‘It is not the case that for all x, if x is a dog then x is not barking.’ |
The Lambda Operator
Kearns doesn’t discuss the lambda operator (or λ-operator). It is also called an abstraction operator or set abstractor. The lambda operator provides a means of representing predicates with an open variable. Given the propositions SWIM(Jill) and LIKE(Jill, Jack), lambda abstraction produces the predicates:
λx(SWIM(x)) i.e. “the set of individuals who swim”
λx(LIKE(x,Jack)) i.e. “the set of individuals who like Jack”
We have defined the meanings of predicates in terms of sets of individuals. Since lambda abstraction just results in a set of individuals it has the effect of producing predicates. In fact, they are referred to as predicate abstracts.
Since λx(SWIM(x)) is just a predicate like all the other predicates in logic, we can apply it to an argument to produce a proposition
λx(SWIM(x))(Jill)
This expression can be read as “Jill is an x such that SWIM(x) is true.” Admittedly, this is just a more complicated way of saying
SWIM(Jill)
In the same manner λx(LIKE(x,Jack))(Jill) is equivalent to LIKE(Jill, Jack). Both of these examples illustrate the process of lambda conversion. Lambda conversion converts any formula of the form λx[...x...](a) to [...a...].
Although lambda abstraction produces more complicated expressions, it has the virtue of bringing the logical expressions into line with ordinary English. For example, the discussion question asks how to express the sentence ‘Jack, Jill really likes’. With the usual predicate logic means at our disposal we are stuck with either
Like(Jill, Jack)
∃x((x = Jack) & Like(Jill, x))
The lambda operator provides another way to express this sentence
λx(LIKE(Jill,x))(Jack)
which is translated as “Jack is an x such that LIKE(Jill,x).”
Richard Montague used lambda abstraction in the Proper Treatment of Quantification in Ordinary English to align the logical expressions with English syntax. Compare the following logical statements with their ordinary English translations
A dog howled ∃x(DOG(x) & HOWL(x))
Every student growled ∀x(STUDENT(x) —> GROWL(x))
In both cases, the ordinary English sentence has a subject predicate structure while the logical translations multiply the number of predicates to express the subject. Montague used lambda abstraction to make assertions about individuals, but about the properties of howling or growling. For example, the first sentence asserts the property of howling has a second-order property of being true of some dog, while the second sentence asserts the property of growling has a second-order property of being true of every student. The lambda expressions can express this idea directly, but this time abstracting the predicate rather than an argument (this is what gives them a “second-order” property). Abstracting the predicate produces a logical translation for the subject (“a dog” and “every student”). The lambda abstractions from our two sentences would be
λP ∃x(DOG(x) & P(x))
λP ∀x(STUDENT(x) —> P(x))
To translate the sentence “A dog howled” we simply add the predicate
λP ∃x(DOG(x) & P(x))(HOWL)
We know this expression is equivalent to ∃x(DOG(x) & HOWL(x)), but it preserves the syntactic structure of the ordinary English sentence. Simple sentences such as “John howls” are understood to assert the property of howling has the second-order property of being true of John, i.e. howling is one of John’s things. In lambda notation this becomes λP(P(j)).
We can pursue this approach a step further and abstract the determiner meaning from the noun phrase translation. If “every student” has the translation λP ∀x(STUDENT(x) —> P(x)) then “every” can be given the translation
λQ λP ∀x(Q(x) —> P(x))
The complete translation for the sentence “every student growled” would be
λQ λP ∀x(Q(x) —> P(x))(STUDENT)(GROWL)
While lambda abstraction brings logical translation into line with the syntactic structure of English, Dowty et al. (1981:110) warns against treating these expressions as a formal level of linguistic representation such as Logical Form. Lambda abstraction merely provides another means of expressing semantic values.
Discussion Questions (de Swart 1998)
1. Consider the sentences in (i) and (ii):
(i) Jill really likes Jack.
(ii) Jack, Jill really likes.
What can you say about the difference in syntactic structure between (i) and (ii)? Translate the two sentences into first-order predicate logic. What can you say about the difference in meaning between (i) and (ii)?
2. Translate the following sentences into first-order predicate logic. Give the key to your translation.
(i) Fido likes someone.
(ii) People who live in New York love it.
(iii) Although no one made any noise, John was annoyed.
(iv) Everything is black or white.
(v) If someone is noisy, he annoys everybody.
(vi) No one answered every question.
(vii) All is well that ends well.
3. Determine whether the following natural language arguments are valid by checking the validity of their predicate-logical counterparts. In order to do so, translate the arguments into first-order predicate logic and give the key for your translation. The parts in parentheses in (iii) provide background information and need not be translated. If the argument is valid, explain which rule(s) of inference show this (remember to use the inference rules from propositional logic if applicable!). If the argument is invalid, provide a counterexample (i.e., describe a situation which makes the premises true, but the conclusion false).
(i) Everyone in the semantics class got an A for their exam. Jim did not get an A for his exam. Therefore, Jim is not in the semantics class.
(ii) Some philosophers are absent-minded. Socrates is a philosopher. So Socrates is absent-minded.
(iii) (There are fifteen students in my class.) Every student passed their exam. Everyone who passed got an A or a B. Some students got an A. So some students got a B or lower.
(iv) Whoever forgives at least one person is a saint. There are no saints. So no one forgives anyone.
Exercises (Kearns 51)
1. Using ∀ and ∃ where appropriate, write logical forms for the sentences below.
a. A young woman arrived.
b. Ida saw something sinister.
c. All roads lead to Rome.
d. Utopia welcomes all travellers from Spain.
e. There’s a castle in Edinburgh.
f. Someone murdered Clive.
g. Nobody saw Charles.
h. Maxine sent every letter John had written her to Ruth.
i. Gina or Boris fed every puppy.
j. Grammar A generates all and only well-formed formulae.
k. Every prize was won by some high school kid.
2. Using ∀ and ∃, write logical forms for the sentences below. If the sentence is ambiguous, give a form for each reading.
a. Everyone doesn’t like Bob.
b. Not everyone likes Bob.
c. Bob doesn’t like everyone.
d. Bob doesn’t like anyone.
References
de Swart, Henriëtte. 1998. Introduction to Natural Language Semantics. Stanford: CSLI Publications.
Dowty, David R., Wall, Robert E. & Peters, Stanley. 1981. Introduction to Montague Semantics. Dordrecht: D. Reidel.
Kutz, Christopher. 2000. Acting Together. Philosophy and Phenomenological Research 61(1): 1-31.
McCawley, James. 1981. Everything that Linguists have Always Wanted to Know about Logic. Chicago: University of Chicago Press.
Montague, Richard. 1973. The proper treatment of quantification in ordinary English. In J. Hintikka, J. Moravcsik, and P. Suppes (eds.), Approaches to Natural Language. Dordrecht: D. Reidel.
Vendler, Zeno. 1967. Linguistics in Philosophy. Ithaca: Cornell University Press.